The Catenary - The Mathematics of a Hanging Chain

Introduction

The catenary is one of the most elegant curves in mathematics and physics. It describes the shape that a uniform chain or cable naturally assumes when suspended between two points under the influence of gravity. While it might seem like a simple problem, the catenary connects deep mathematical concepts and provides a nice example of using physics intution to solve problems.

The Physical Problem

The set-up of this problem is very simple: simply take a chain of length $L$ with some uniform mass density $\rho$ and suspend this between two points that are (at least for now) at an equal height. See the diagram drawn below:

Mathematical Derivation

There are two ways to derive the catenary equation. The first and most simple approach uses a balance of forces on a segment of the chain. This is a classic high school physics problem… lets quickly sketch out the solution:

Setting Up the Problem: Balance of Forces

The first way of solving this problem is with a balance of forces on the chain. Consider a segment of the chain from the bottom (where the chain is horizontal) to some point along the curve. The unknown quantities of our problem are then simply:

• $T_0$: The horizontal tension at the bottom of the chain
• $T_1$: The tension at the upper end of the segment, acting along the tangent to the chain
• $W$: The weight of the segment, acting downward
• $\theta$: The angle that $T_1$ makes with the horizontal

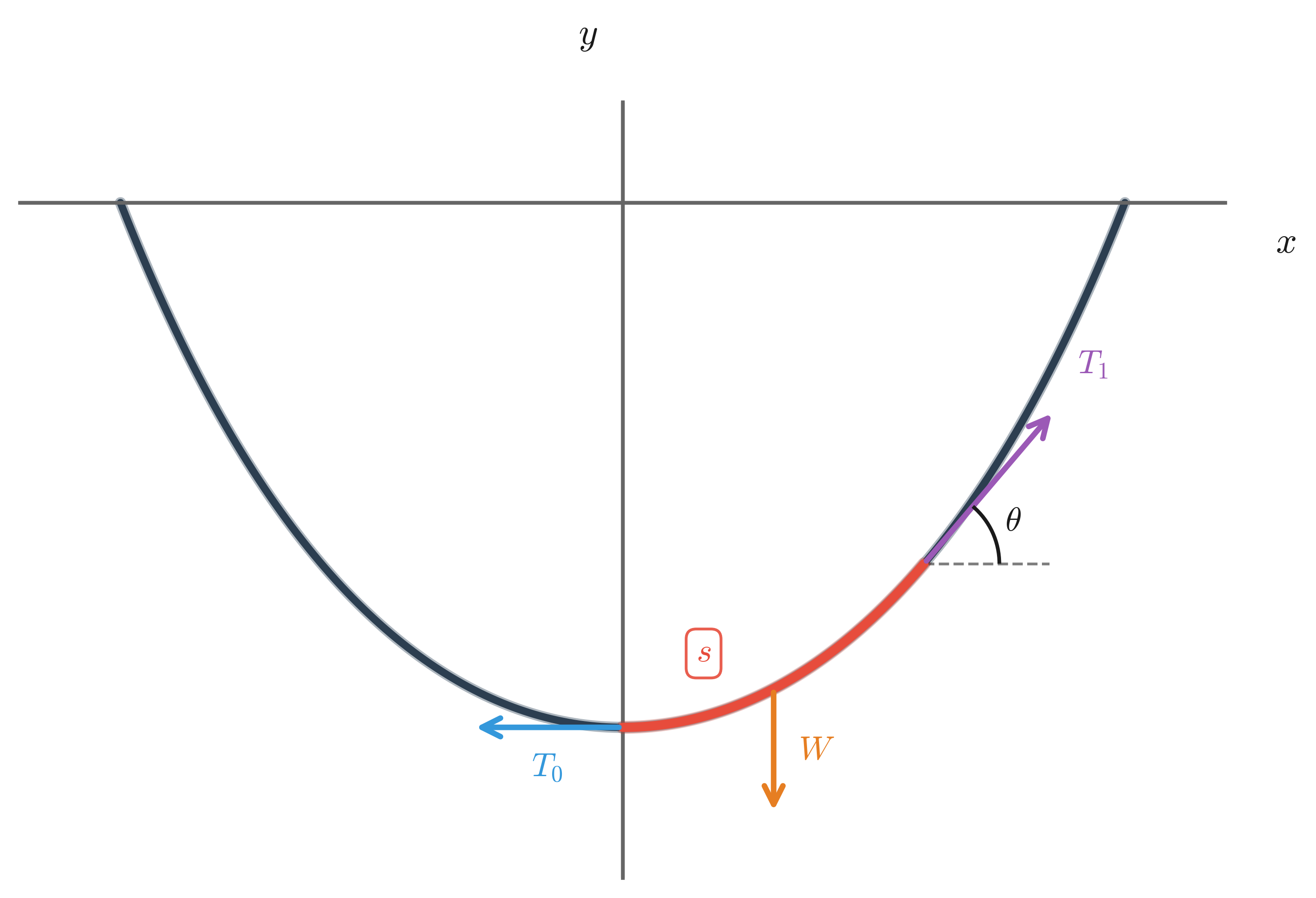
[To be filled: Derivation using force balance equations]

The Variational Approach

[To be filled:

• Minimizing potential energy
• Euler-Lagrange equation
• Derivation of the differential equation]

Solving the Differential Equation

[To be filled:

• The catenary equation: y = a cosh(x/a)
• Physical meaning of the parameter ‘a’
• Boundary conditions]

Physical Intuition

[To be filled:

• Why the catenary shape minimizes potential energy
• The role of tension
• Comparison with other curves (parabola, circular arc)]

Key Properties

[To be filled:

• The catenary is self-similar
• Relationship between sag and span
• Tension distribution along the curve]

Applications

[To be filled:

• Suspension bridges
• Power lines - Other engineering applications]

Visualizations

[To be filled: Link to Jupyter notebook with animations showing:

• How the catenary shape changes with different parameters
• Comparison with parabola
• Dynamic visualization of the hanging chain
• Interactive exploration of boundary conditions]

Beyond the Simple Case

[To be filled:

• Catenary with different endpoint heights
• Catenary with non-uniform density
• Catenary under additional loads (e.g., suspension bridges)]

Conclusion

[To be filled: Summary of key insights and the beauty of the mathematical solution]

Further Reading

[To be filled: References and resources for deeper exploration]